


INSTITUTO TECNOLOGICO SUPERIOR DE SAN MARTIN TEXMELUCAN
MATERIA: CALCULO INTEGRAL
PROF: HECTOR GABRIEL MENDEZ LARA
INTEGRANTES:
Maria De Lourdes Lopez Ramos
Claudia Caballero Meza
Alejandro Rodriguez Estevez
Ilse Veronica Roque Perez
Claudia Caballero Meza
Alejandro Rodriguez Estevez
Ilse Veronica Roque Perez
2°"B"ISC
LIGAS:
INTEGRAL INDEFINIDA
POR PARTES
POR SITUACION TRIGONOMETRICA
INTEGRALES DIRECTAS
Integración por fracciones parciales
Integrales por sustitución o cambio de variable
LA INTEGRAL INDEFINIDA
Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII .
Aunque la utilidad del cálculo integral es alta y variada, ésta no se presentará con toda su fuerza hasta tomar contacto con la integral definida. El objetivo de este tema y del siguiente es mostrar las técnicas más comunes para el cálculo de integrales más o menos sencillas; una vez conocidas estas técnicas, llegará el momento de explotar su uso en el cálculo de áreas y volúmenes.
FUNCIÓN PRIMITIVA DE UNA FUNCIÓN
Dada una función cualquiera f(x) definida en un intervalo cerrado [a,b], se llama función primitiva de f(x) a otra función F(x) cuya derivada sea f(x) en dicho intervalo. Es decir, F'(x) = f(x) para todo x de [a,b].
Así:
La función sen x es una primitiva de cos x puesto que (sen x)' = cos x.

PROPIEDADES
Primera propiedad
Si F(x) es una primitiva de f(x) y C una constante cualquiera (un número), la función
F(x) + C es otra primitiva de f(x).
Demostración:
Basta recordar que la derivada de una suma de funciones es igual a la suma de las derivadas de las funciones, y que la derivada de una constante es siempre cero.
(F(x) + C)' = F'(x) + C' = f(x) + 0 = f(x)
Ejercicio: primitivas de una función
Encontrar tres primitivas de la función cos x.
Resolución:
ð Se sabe que sen x es una primitiva de cos x.
ð Tres primitivas de cos x son, por ejemplo,
Si una función tiene una primitiva, entonces tiene infinitas primitivas.
Demostración:
Si F(x) es una primitiva de f(x), para cualquier constante C, F(x) + C es otra primitiva según la anterior propiedad. Así, hay tantas primitivas como valores se le quieran dar
a C.
Tercera propiedad
Dos primitivas de una misma función se diferencian en una constante. Esto es, si F(x) y G(x) son primitivas de la función f(x), entonces F(x) - G(x) = C = cte.
Demostración:
Hay que recordar que si una función f(x) definida en un intervalo cualquiera tiene derivada cero en todos los puntos, entonces la función f(x) es constante. Es decir, si f'(x) = 0, entonces f(x) = C.
Pues bien, si F(x) es una primitiva de f(x), F'(x) = f(x);
si G(x) es otra primitiva de f(x), G'(x) = f(x).
Restando miembro a miembro, F'(x) - G'(x) = (F(x) - G(x))' = f(x) - f(x) = 0, de donde se deduce que F(x) - G(x) = C.
INTEGRAL INDEFINIDA DE UNA FUNC.
Se llama integral indefinida de una función f(x), al conjunto de todas las primitivas de la función f(x), y se simboliza
Esta expresión se lee «integral de efe de equis diferencial de equis».
Por las propiedades de la función primitiva, si F(x) es una primitiva de f(x),
donde C representa una constante llamada constante de integración.
Ejercicio: cálculo de primitivas
Resolución:
ð Puesto que una primitiva de cos x es sen x,
Resolución:
Por consiguiente,
Resolución:
Integración por cambio de variable (o sustitución)
Este método consiste en transformar la integral dada en otra más sencilla mediante un cambio de la variable independiente. Aunque algunos casos tienen un método preciso, es la práctica, en general, la que proporciona la elección del cambio de variable más conveniente.
Se comenzará por estudiar aquellas integrales que son casi inmediatas.
Si en lugar de x se tuviese una función u(x), x → u(x) → u(x)m , la regla de la cadena
Por tanto,
Como se ve, se ha escrito u en lugar de u(x) por simplificar la notación.
EJEMPLOS:
Resolución:
Resolución:
ð Sin embargo, en la integral no se tiene 2x sino x. Este contratiempo se 
por la constante (en este caso 2) que falta.
Resolución:
Resolución:
ð Se multiplica y se divide por 3:


Si en lugar de x se tuviese una función de x, u(x), la derivada de ln | u(x) |, por la regla de
Ejercicio: cálculo de integrales por cambio de variable
Resolución:
ð Se multiplica y se divide por 6:
Resolución:
Por tanto,
El cambio de variables es uno de los métodos más usados en la integración. Permite expresar la integral inicial mediante un nuevo integrando y un nuevo dominio siendo la integral equivalente a la primera. Para integrales simples de una sola variable si  es la variable original y
es la variable original y 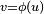 es una función invertible, se tiene:
es una función invertible, se tiene:
 es la variable original y
es la variable original y 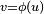 es una función invertible, se tiene:
es una función invertible, se tiene:Ejemplo 1






Ejemplos 2
























EJEMPLO 3






Integrales de funciones trigonométricas
Con carácter general un cambio que resulta muchas veces útil expresar las potencias funciones trigonométricas mediante funciones de ángulos múltiples, eso pude lograrse gracias a las siguientes identidades:
Por ejemplo las dos fórmulas anteriores permiten substituir potencias complejas de la función coseno por el coseno de ángulos múltiplo:
Integral que contiene potencias de senos y cosenos 
- En general, se intenta escribir un integrando en el que intervienen potencias de seno y coseno en una forma donde se tiene sólo un factor seno (y el resto de la expresión en términos de coseno) o sólo un factor coseno (y el resto de la expresión en términos de seno).
- La identidad sin 2x + cos 2x = 1 permite convertir de una parte a otra entre potencias pares de seno y coseno.
- Existen 3 casos:
Cuando n es impar
Cuando  , podemos apartar un factor del seno y sustituirlo por la identidad sin 2x = 1 − cos 2x para poder expresar los factores restantes en términos del coseno:
, podemos apartar un factor del seno y sustituirlo por la identidad sin 2x = 1 − cos 2x para poder expresar los factores restantes en términos del coseno:
 , podemos apartar un factor del seno y sustituirlo por la identidad sin 2x = 1 − cos 2x para poder expresar los factores restantes en términos del coseno:
, podemos apartar un factor del seno y sustituirlo por la identidad sin 2x = 1 − cos 2x para poder expresar los factores restantes en términos del coseno:
Al tener el integral de esta forma se puede resolver por medio de sustitución haciendo u = cos(x), du = − sin(x)dx. Como en la expresión no tenemos un − sin(x)dx multiplicamos ambos lados por ( − 1) y nos queda la expresión − du = sin(x)dx que ya podemos sustituir:
Cuando m es impar
Cuando m = 2k + 1, podemos de la misma manera apartar un factor de coseno y emplear cos 2x = 1 − sin 2x para poder expresar los factores restantes en términos del sin x:
al hacer u = sin x y du = cos xdx tendríamos
Cuando m y n son pares
Cuando dichas potencias son pares a la vez n = 2k y m = 2p, podemos aplicar las identidades de la mitad de ángulo:
algunas veces es útil usar la identidad:
sería igual a:
Ejemplo #1
- Solución Lo primero que tenemos que ver es que la potencia impar la tiene la función seno, esto nos hace notar que estamos en el primer caso que describimos arriba, entonces aplicamos el algoritmo,
Sustituyendo u = cos x , tenemos du = − sin xdx luego:
Integrales que contiene potencias de tangentes y secantes
- Se puede usar una estrategia similar a la anterior.
- Puesto que:
-
 , se puede separar un factor sec 2x y convertir la potencia restante (par) de la secante en una expresión relacionada con la tangente por medio de la identidad sec 2x = 1 + tan 2x.
, se puede separar un factor sec 2x y convertir la potencia restante (par) de la secante en una expresión relacionada con la tangente por medio de la identidad sec 2x = 1 + tan 2x.
-
- O bien, puesto que:
-
 , se puede separar un factor sec xtan x y convertir la potencia restante (par) de tangente a secante.
, se puede separar un factor sec xtan x y convertir la potencia restante (par) de tangente a secante.
-
- Existen 3 casos:
Cuando n es par
n = 2k separar un factor de sec 2x y utilice sec 2x = 1 + tan 2x para lograr expresar los factores restantes en términos de tan x:
de esta manera podemos hacer u = tan x y du = sec2xdx y el integral quedaría así:
Cuando m es impar
m = 2k + 1 apartar un factor de sec xtan x y emplear tan 2x = sec 2x − 1 para poder expresar los factores que restan en términos de sec x:
de esta manera se puede hacer u = sec x y  , con lo que queda
, con lo que queda
 , con lo que queda
, con lo que queda
La tangente tiene potencia par 
La Secante tiene potencia impar
En este caso se procede a integrar por partes.
Ninguno de los anteriores
Al no encontrar la forma de ninguno de los pasos anteriores, se traslada a senx y cosx, recordando que:
Para otros casos, las directrices no son tan claras. Podría ser necesario usar identidades, integración por partes y, ocacionalmente, un poco de inventiva.
- A veces será necesario poder integrar tan x por medio de la fórmula establecida:
- Se necesitará también la integral indefinida de la secante:
Esta última se podría comprobar mediante la derivación de lado derecho, o como sigue:
- Primero se mutiplican numerador y denominador por sec x + tan x :
- Si se sustituye u = sec x + tan x, después du = (sec xtan x + sec 2x)dx, también, la integral se convierte en:
- Así, se tiene:
- NOTA: Para integrales que contienen cosecantes y cotangentes, la estrategia es análoga a la del par secantes-tangentes. Recordar la identidad:
csc 2x = 1 + cot 2x
EJEMPLOS
1

2 






























EJEMPLOS
1
3 
4 

5 


6 

7 





8 

9 



10 

11

12 


13 


14 
15 

Integración directa
En ocasiones es posible aplicar la relación dada por el teorema fundamental del cálculo de forma directa. Esto es, si se conoce de antemano una función cuya derivada sea igual a f(x) (ya sea por disponer de una tabla de integrales o por haberse calculado previamente), entonces tal función es el resultado de la antiderivada. La integración directa requiere una confeccionar una tabla de funciones y sus antidervidas o funciones primitivas.
EJEMPLOS
EJEMPLOS
- Ejemplo
- Calcular la integral indefinida
 .
.
- Ejemplo
- Calcular la integral indefinida
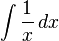 .
. - Una fórmula estándar sobre derivadas establece que
 . De este modo, la solución del problema es
. De este modo, la solución del problema es  .
.
No obstante, puesto que la función  esta definida en los números negativos también ha de estarlo su integral, así que, la integral escrita de una forma rigurosa sería ln(|x|)
esta definida en los números negativos también ha de estarlo su integral, así que, la integral escrita de una forma rigurosa sería ln(|x|)
 esta definida en los números negativos también ha de estarlo su integral, así que, la integral escrita de una forma rigurosa sería ln(|x|)
esta definida en los números negativos también ha de estarlo su integral, así que, la integral escrita de una forma rigurosa sería ln(|x|)
La derivada de ex es la propia función ex . Si en lugar de x se tuviese una función
u( x ), la derivada de eu( x ) por la regla de la cadena es eu( x ) · u' ( x ).
Por consiguiente,
Método de integración por partes
El método de integración por partes es el que resulta de aplicar el siguiente teorema:
.
Existen diversos dichos mnemotécnicos para recordar la integración por partes, la cual dice así:
- "Sentado (
 ) un día vi, un valiente soldado (
) un día vi, un valiente soldado ( ) vestido de uniforme" .
) vestido de uniforme" . - "Un día vi un viejo sin bastón vestido de uniforme".
- "un viejo soldado(-integral) vestido de uniforme" .
- "Unamuno dice verdades: una verdad menos integra verdaderas dudas universales" .
- Para elegir la función
 se puede usar una de las siguiente reglas mnemotécnicas:
se puede usar una de las siguiente reglas mnemotécnicas:
- Arcoseno, arcocoseno..., Logarítmicas, Polinómicas, Exponenciales, Seno, coseno, tangente... ⇒ A L P E S.
- Nota: Elegimos siempre "u" como la función situada más a la izquierda de la palabra ALPES.
- Inversas trigonométricas, Logarítmicas, Algebráicas, Trigonométricas, Exponenciales. ⇒ I L A T E.
- Nota: Elegimos siempre "u" como la función situada más a la izquierda de la palabra ILATE.
- Inversas trigonométricas, Logarítmicas, Potenciales, Exponenciales, Trigonométricas ⇒ I L P E T
- Nota: Elegimos siempre "u" como la función situada más a la izquierda de la palabra ILPET.
Ejemplo 1.
Encuentre ∫ x cos(x) dx
Solución.
Con el fin de utilizar la fórmula anterior, tomaremos f(x) = x y g'(x) = cos(x), es
decir el integrando xcos(x) = f(x) g'(x)
f(x) = x g '(x) = cos(x)
f(x) = 1 g(x) = sen(x)
∫ x cos(x) dx = xsen(x) − ∫ sen(x) dx = − xsen(x) + cos(x) + c
Observe que también hubiéramos podido hacer la siguiente elección de f y g':
f (x) = cos(x) g '(x) = x
f (x) = -sen(x) g(x) = x2/2
sólo que la función por integrar en el lado derecho tiene un mayor grado de dificultad para
NOTACIÓN. Con el fin de ser congruentes con la notación utilizada en la mayoría de los
libros del mercado, le llamaremos
u = f(x) y v = g(x) y en consecuencia du = f '(x)dx así como du = g '(x)dx. Con esta
nueva notación resolveremos los siguientes ejercicios.
Ejemplo 2.
Encuentre ∫ xex dx
Solución. Utilizaremos el siguiente cuadro
u = x v = ex
du = dx dv = ex dx
obsérvese que con esta notación, en vez de tomar
g' (x) = ex , tomamos su diferencial
dv = ekdx y análogamente con f, permitiendo que una parte del integrando sea u y el resto
sea
dv.
∫ xex dx = xex − ∫ex dx = xex − ex + c
En estos primeros dos ejemplos, una adecuada elección de
u y dv nos lleva en un solo paso
a resolver nuestra integral reduciéndola a una integral más fácil de resolver.
Existen otras situaciones, como se verá en los siguientes ejemplos, en que si bien la integral
del lado derecho tiene un menor grado de dificultad, no es una integral inmediata, requiere
de un nuevo proceso de integración por partes ó resolverla por cambio de variable, ó algún
otro procedimiento.Ejemplo 3. Encuentre ∫ x2ex dx
Solución.
Utilizaremos el siguiente cuadro
u = x2 v = ex
du = 2xdx dv = ex dx
∫ x2ex dx = x2ex − 2∫ xex dx
la integral del lado derecho se resuelve por partes (Ejemplo 2), obteniendo:
∫ x2ex dx = x2ex − 2(xex − ex ) + c
Observación
: La elección u = ex, dv = x2dx nos lleva a una integral con un mayor grado de
dificultad.
Integrales por situacion trigonometrica
 ,
,  y
y 
Este método se basa en el uso de triángulos rectángulos, el teorema de Pitágoras e identidades trigonométricas.
En el caso general la integral a resolver es:
Simplifiquemos paso a paso el termino de la raíz, primeramente sacaremos a factor común, y operaremos para poder dejarlo como suma de cuadrados.

De esta forma estaremos en tres situaciones posibles:
- a > 0 Λ
 es decir:
es decir: 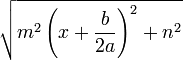
- a > 0 Λ
 es decir:
es decir: 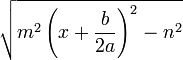
- a < 0 Λ
 es decir:
es decir: 
teniendo la forma las ecuaciones conocidas: con

Estos los cambios que hay que realizar según la situación:
Ejemplo






Ejemplos























Fracción parcial
El método de las fracciones parciales consiste en descomponer un cociente de polinomios en una suma de fracciones de polinomios de menor grado. Se utiliza principalmente en cálculo integral. El requisito más importante es que el grado del polinomio del denominador sea estrictamente mayor que el del numerador.
Características
Para mayor claridad, sea:
en donde:  . Para reducir la expresión a fracciones parciales se debe expresar la función
. Para reducir la expresión a fracciones parciales se debe expresar la función 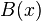 de la forma:
de la forma:
 . Para reducir la expresión a fracciones parciales se debe expresar la función
. Para reducir la expresión a fracciones parciales se debe expresar la función 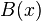 de la forma:
de la forma: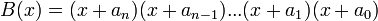
- o

Casos
Se distinguen 4 casos:
Factores lineales distintos
Donde ningún par de factores es idéntico.
Donde  son constantes a determinar, y ningún denominador se anula.
son constantes a determinar, y ningún denominador se anula.
 son constantes a determinar, y ningún denominador se anula.
son constantes a determinar, y ningún denominador se anula.Factores lineales repetidos
Donde los pares de factores son idénticos.
Donde  son constantes a determinar, y ningún denominador se anula.
son constantes a determinar, y ningún denominador se anula.
 son constantes a determinar, y ningún denominador se anula.
son constantes a determinar, y ningún denominador se anula.Factores cuadráticos distintos
Donde ningún par de factores es idéntico.
Donde  son constantes a determinar, y ningún denominador se anula.
son constantes a determinar, y ningún denominador se anula.
 son constantes a determinar, y ningún denominador se anula.
son constantes a determinar, y ningún denominador se anula.Factores cuadráticos repetidos
Donde  son constantes a determinar, y ningún denominador se anula..
son constantes a determinar, y ningún denominador se anula..
 son constantes a determinar, y ningún denominador se anula..
son constantes a determinar, y ningún denominador se anula..
Observación: Es posible construir ejemplos que combinan los cuatro casos anteriores.
Cómputo de las constantes
Para hallar las constantes, en el caso de factores lineales distintos se puede utilizar la siguiente fórmula:
en donde 

Para los otros casos no existe una formulación específica. Sin embargo, estos se pueden resolver simplificando y formando un sistema de ecuaciones con cada una de las  , la resolución del sistema proporciona los valores de los
, la resolución del sistema proporciona los valores de los  .
.
 , la resolución del sistema proporciona los valores de los
, la resolución del sistema proporciona los valores de los  .
.
EJEMPLOS
Integración por fracciones parciales ejemplo 1
 |
 |
 |
 |
 |
 |
 |
 |
 |
Integración por fracciones parciales ejemplo 2
Esto es lo que usted escribira:
x^2 / (x^2 - 1)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Integración por fracciones parciales ejemplo 3
Esto es lo que usted escribira:
x^3 / (x^2 - 1)
 |
 |
 |
 |
 |
 |
 |
 |
 |
Integración por fracciones parciales ejemplo 4
Esto es lo que usted escribira:
1 / (x^2 + 1)
 |
Integración por fracciones parciales ejemplo 5
Esto es lo que usted escribira:
x^2 / (x^2 + 1)




Integración por fracciones parciales ejemplo 5
Esto es lo que usted escribira:
x^2 / (x^2 + 1)






![\begin{matrix} \cos^{2n+1} x = \left( \frac{e^{ix}+e^{-ix}}{2}\right)^{2n+1} =
\cfrac{1}{2^{2n}}
\sum_{k=0}^n \begin{pmatrix} 2n+1 \\ k \end{pmatrix} \cos{(2k+1)x} \\
\cos^{2n} x = \left( \frac{e^{ix}+e^{-ix}}{2}\right)^{2n} =
\cfrac{1}{2^{2n-1}} \left[1 +
\sum_{k=1}^n \begin{pmatrix} 2n \\ k \end{pmatrix} \cos{(2k)x} \right] \end{matrix}](http://upload.wikimedia.org/wikipedia/es/math/4/c/0/4c0f77b69cdf5ed76b00954ac1074829.png)
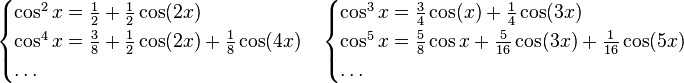









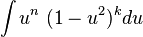
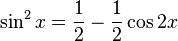


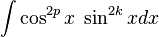

![\int [\frac{1}{2} + \frac{1}{2}\cos 2x]^{p}\;
[\frac{1}{2} - \frac{1}{2}\cos 2x]^{k} dx](http://upload.wikimedia.org/wikipedia/es/math/f/8/a/f8ad147bc91a1a82fa5309934f92f7e2.png)
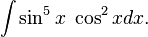






![\int [1 + \tan^{2}x]^{k-1}\;tan^{m}x\;sec^{2}xdx](http://upload.wikimedia.org/wikipedia/es/math/3/0/8/30866643a2d7aceb9095b9b2f73a34fd.png)
![\int [1 + u^{2}]^{k -1}\;u^mdu](http://upload.wikimedia.org/wikipedia/es/math/e/3/e/e3e2074f101e0aecf783fb20fc3fc5a4.png)
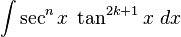
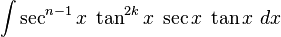
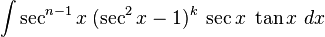


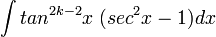





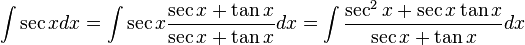



 y
y  , puede simplificarse mucho la resolución de la
, puede simplificarse mucho la resolución de la 




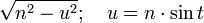





![A_k = \left[\frac{A(x)}{B(x)}(x+a_k)\right]_{x=-a_k}](http://upload.wikimedia.org/wikipedia/es/math/7/d/7/7d7cff0527d60988fff19766153bd0df.png)

No hay comentarios:
Publicar un comentario